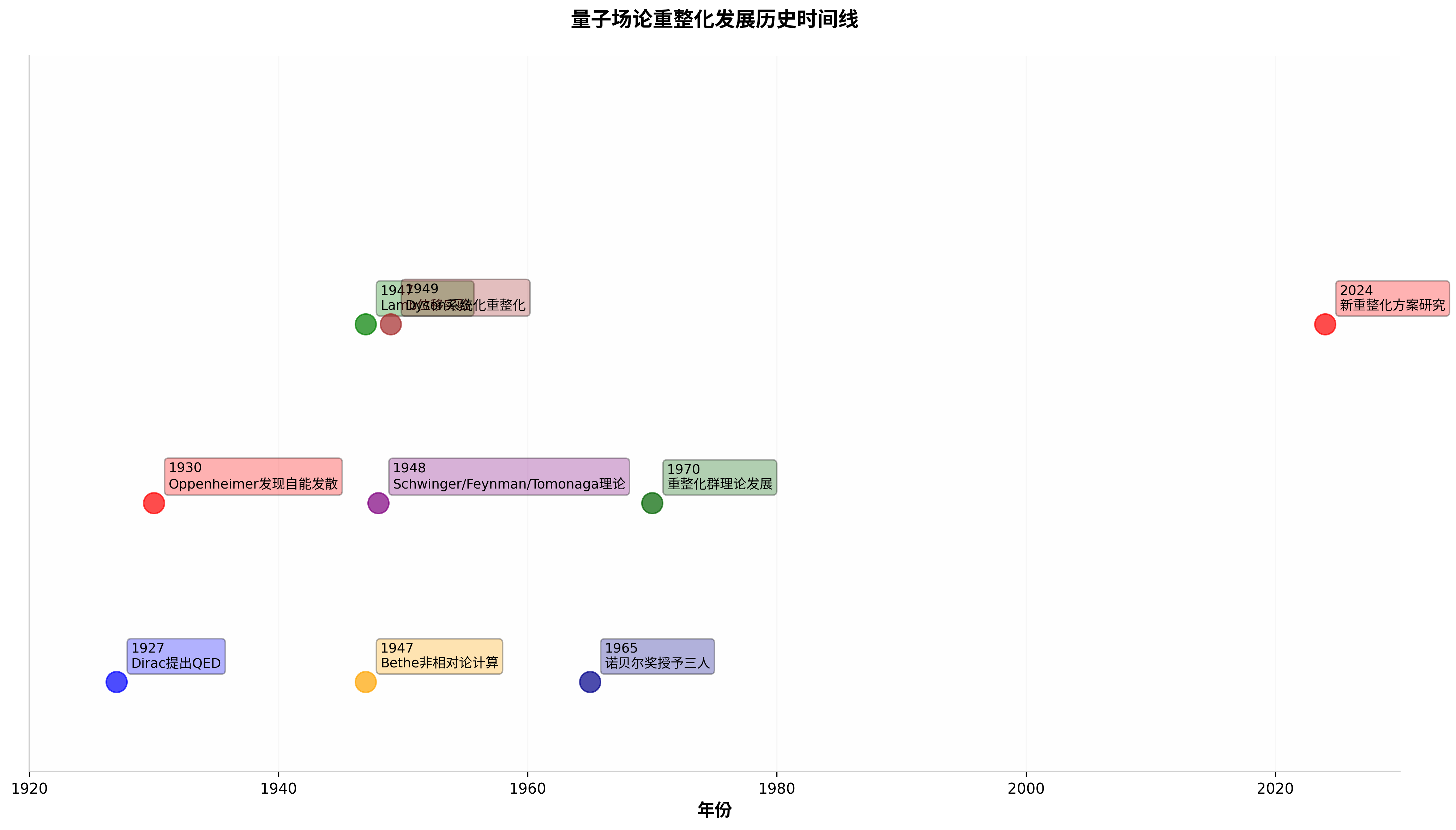
I. 量子场论中的无穷大问题：历史与根源

1927
Dirac提出QED
1930
Oppenheimer发现发散
20年
问题未解决时期

1.1 问题的起源

1927
Dirac的革命性论文
保罗·狄拉克发表《辐射的量子理论》，首次提出量子电动力学（QED）的概念，奠定了量子场论的基础。
1930
Oppenheimer的发现
罗伯特·奥本海默在计算原子电子与量子电磁场相互作用时，发现电子自能发散，这是量子场论中第一个严重的无穷大问题。
1930s
Weisskopf的改进
维克托·魏斯科普夫通过考虑虚电子-正电子对产生的影响，部分抵消了最糟糕的发散，但仍留下对数发散。

发散的物理意义

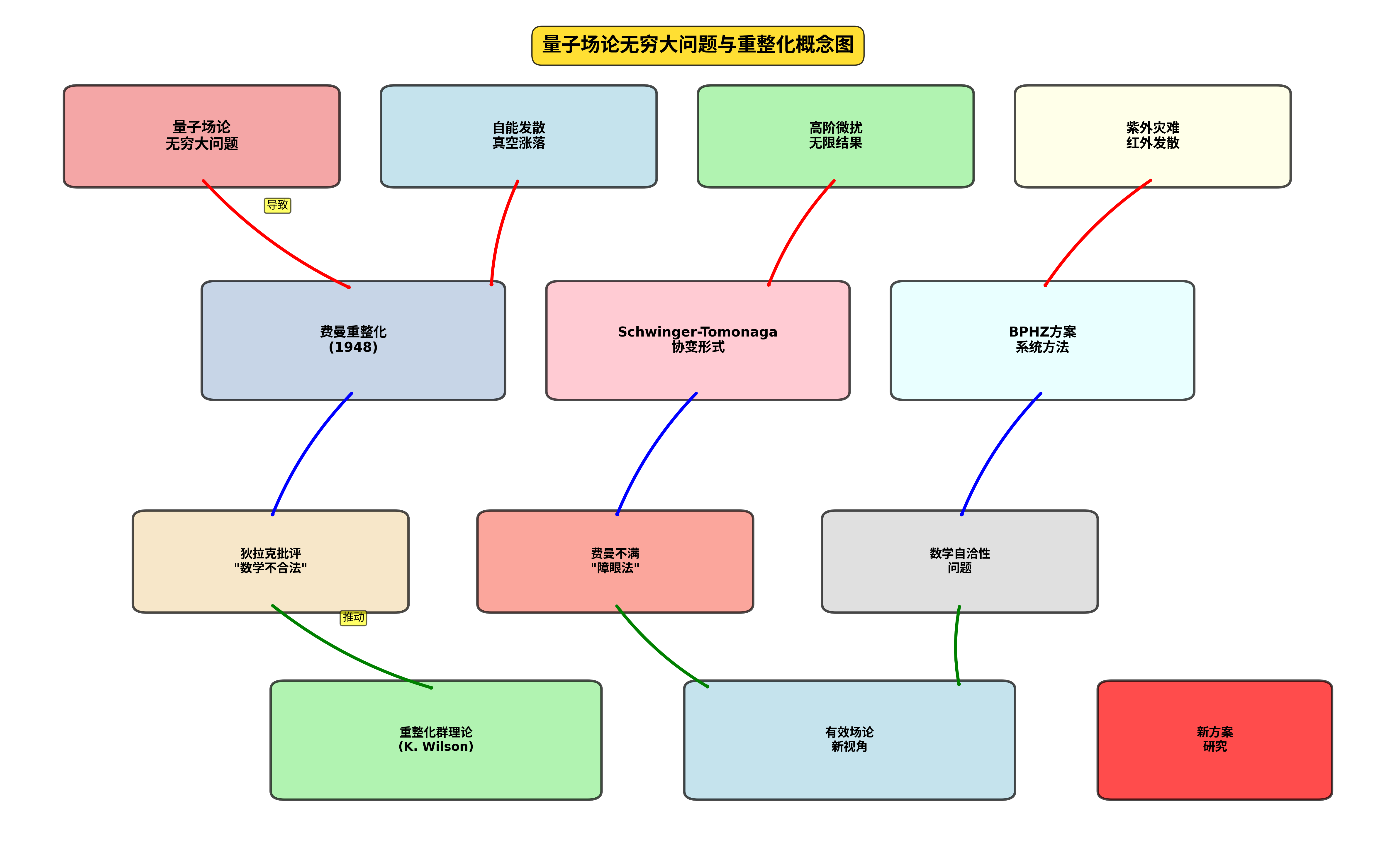
这些无穷大并非简单的数学错误，而是反映了量子场论在短距离（高能量）尺度上的根本困难。它们暗示着理论可能需要修改或重新解释。

1.2 发散的类型

重整化发展历史时间线
图1：量子场论重整化发展历史时间线
  • 紫外发散：与短距离、高动量相关的发散，类似于经典电子的无限自能
  • 红外发散：与长距离、低动量相关的发散，通常与零质量粒子有关
  • 真空涨落：量子场的零点能无限大，但不影响可观测的能量差

自能发散的数学表达

在量子电动力学中，电子自能修正可以表示为：

Σ(p) = ∫ d⁴k / (k² - m² + iε) × 1/((p-k)² - m² + iε)

这个积分在大动量（k → ∞）时表现为对数发散：

Σ(p) ∼ log(Λ/m)

其中Λ是动量截断，m是电子质量。

II. 费曼重整化技术：突破与局限

概念关系图
图2：量子场论无穷大问题与重整化概念关系图

2.1 历史转折点：1947年Shelter Island会议

关键实验发现：1947年，威利斯·兰姆和罗伯特·雷瑟福使用微波技术精确测量了氢原子能级，发现2s和2p态之间存在约1057.8 MHz的能量差，这与狄拉克理论的预测不符。这一"兰姆位移"成为推动理论发展的关键实验事实。

"在从Shelter Island会议返回的火车上，我进行了第一个非相对论性的兰姆位移计算。尽管计算有限制，但结果与实验吻合得很好。"
—— 汉斯·贝特

2.2 三位物理学家的贡献

费曼
路径积分与费曼图
施温格
协变算符形式
朝永
多时理论

费曼图的基本规则

费曼图提供了一种图形化的方法来计算量子场论中的散射振幅：

  • 外线：代表入射和出射粒子
  • 内线：代表虚粒子传播
  • 顶点：代表相互作用点
  • 圈图：代表量子修正，通常导致发散

每个图形元素对应一个数学表达式，通过费曼规则可以系统地计算任意过程的振幅。

2.3 重整化的核心思想

关键洞察

重整化的核心在于认识到：理论中的"裸"参数（裸质量、裸电荷）是不可观测的。我们能够测量的只是"物理"的、重整化的参数。通过将无穷大吸收到参数的重定义中，理论可以产生有限的、可检验的预言。

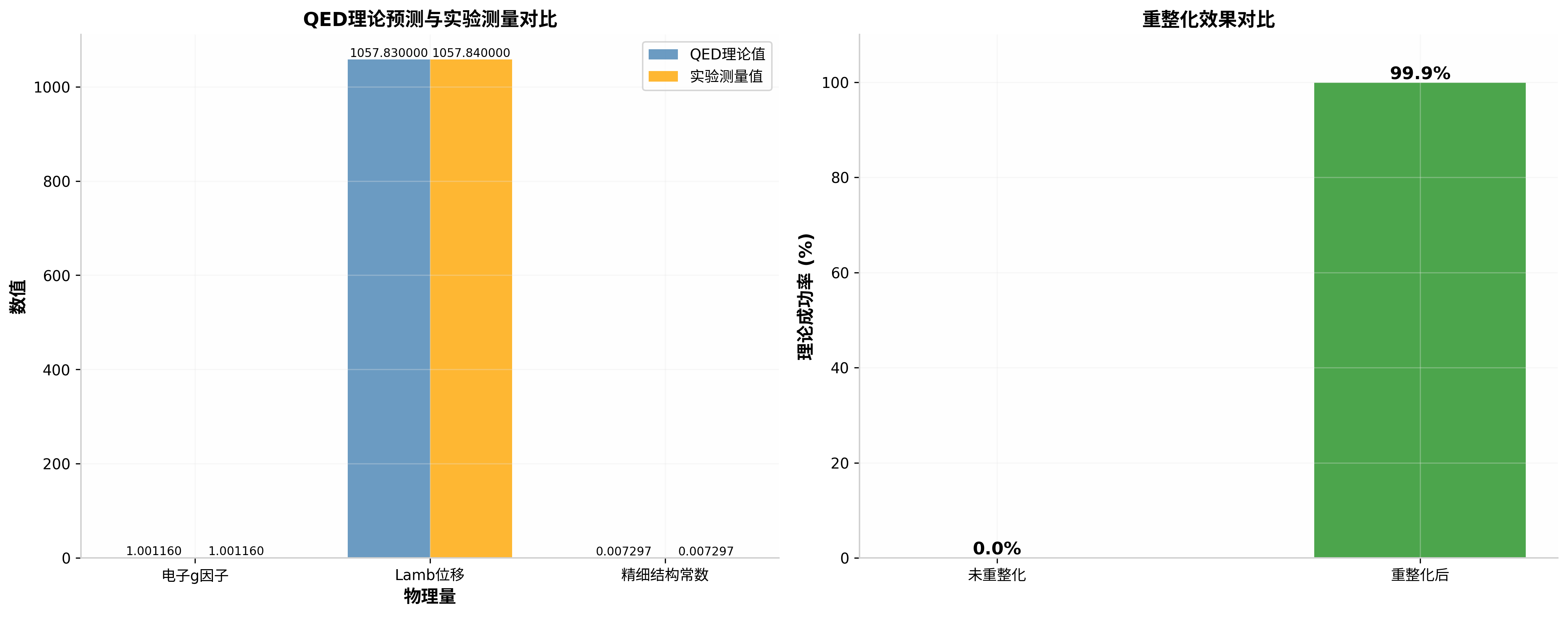
精度对比图
图3：QED理论预测精度与重整化效果对比

2.4 惊人的成功：理论与实验的精确吻合

10⁻¹⁰
电子g因子理论精度
12位
小数点后吻合位数
99.9%
理论成功率
"重整化理论使得QED的微扰计算可以达到任意阶，并且计算结果与实验的吻合程度可以达到小数点后十几位。这使得可重整性成为量子场论的基本要求。"
—— 物理学界的共识

III. 狄拉克与费曼的不满：深层质疑

3.1 狄拉克的持久批评

保罗·狄拉克作为量子力学的奠基人之一，对重整化方法始终持批评态度。即使在1975年，他仍然表示：

"大多数物理学家对这个情况很满意。他们说：'量子电动力学是一个很好的理论，我们不需要再担心它了。'我必须说我对此非常不满意，因为这个所谓的'好理论'确实涉及忽略方程中出现的无穷大，以一种任意的方式忽略它们。这不是合理的数学。合理的数学涉及在数量很小的时候忽略它——而不是仅仅因为它无限大而你又不想要它就忽略它！"
—— 保罗·狄拉克 (1975)

3.2 费曼的矛盾态度

具有讽刺意味的是，尽管费曼是重整化技术的主要贡献者之一，但他本人对这个方法也深感不满：

"我们玩的这个壳牌游戏在技术上被称为'重整化'。但不管这个词多么聪明，我仍然会称它为愚蠢的过程！不得不求助于这种障眼法阻止了我们证明量子电动力学理论在数学上是自洽的。令人惊讶的是，这个理论至今还没有被证明是自洽的；我怀疑重整化在数学上是不合法的。"
—— 理查德·费曼 (1985)

3.3 批评的深层原因

数学上的担忧

  • 发散级数：重整化涉及处理发散的积分和级数，这在严格数学中是不允许的
  • 减除程序：从无穷大中减去无穷大得到有限结果，这在数学上是不明确的操作
  • 非唯一性：重整化方案的选择似乎具有任意性，不同的方案应该给出相同的物理结果，但证明这一点很困难
  • Landau极点：费曼担心的另一个问题是，在所有已知的场论中，相互作用在足够短的距离尺度上变得无限强

3.4 其他物理学家的观点

早期普遍不满：在1940年代末到1960年代，大多数物理学家对重整化持保留态度。Freeman Dyson证明了这些无穷大是基本的，不能通过任何形式数学程序消除。

态度转变：1970年代后，特别是Kenneth Wilson的工作之后，物理学界的态度开始改变。重整化群理论为理解重整化提供了新的视角。

IV. 现代理解：有效场论与重整化群

4.1 Kenneth Wilson的革命性贡献

诺贝尔奖级贡献

Kenneth Wilson在1970年代发展的重整化群理论彻底改变了我们对量子场论中无穷大的理解。他因此获得了1982年诺贝尔物理学奖。

"重整化群提供了一个框架，在这个框架中，短距离截断的存在是自然的。场论只是物质行为的有效、平滑的表示；由于截断总是有限的，所以没有真正的无穷大问题。"
—— Kenneth Wilson

4.2 有效场论的新视角

有效
所有场论都是有效场论
截断
自然存在短距离截断
未知
短距离物理细节不重要

有效场论的基本观点

有效场论观点认为，任何物理理论都有其适用范围：

  • 能量尺度分离：低能现象主要由低能自由度决定
  • 高能自由度：高能自由度的具体细节对低能物理影响有限
  • 参数化：高能效应可以通过有效参数来表示
  • 可预测性：即使不知道短距离物理，仍然可以做出低能预测

这种观点为重整化提供了自然的解释：我们不是在"消除无穷大"，而是在参数化我们对短距离物理的无知。

4.3 凝聚态物理的启示

在凝聚态物理中，重整化群方法被广泛应用于研究临界现象。关键的洞察是：在相变点，系统表现出尺度不变性，这可以用重整化群的不动点来描述。这种成功为高能物理中的重整化提供了类比和支持。

4.4 数学严格化的进展

1970s
构造性量子场论
尝试从数学上严格构造量子场论模型，证明其存在性和性质。
1980s
代数量子场论
使用C*代数和局部量子物理的框架，提供数学上更严格的处理。
1990s
Epstein-Glaser方法
基于因果性的方法，避免了传统重整化中的发散问题。

V. 贾连宝的突破性贡献：UV-Free Scheme

重要发现：2026年《理论物理通讯》发表论文

贾连宝在2026年《理论物理通讯》第78卷发表的论文"Tamed loops: a way to obtain finite loop results without UV divergences"中，提出了一种革命性的UV-Free Scheme方法，能够直接获得有限的环积分结果，无需通过传统重整化的∞−∞操作。

2026
发表年份
UV-Free
方案名称
125 GeV
Higgs质量预测

5.1 核心思想：避免∞−∞的革命性方法

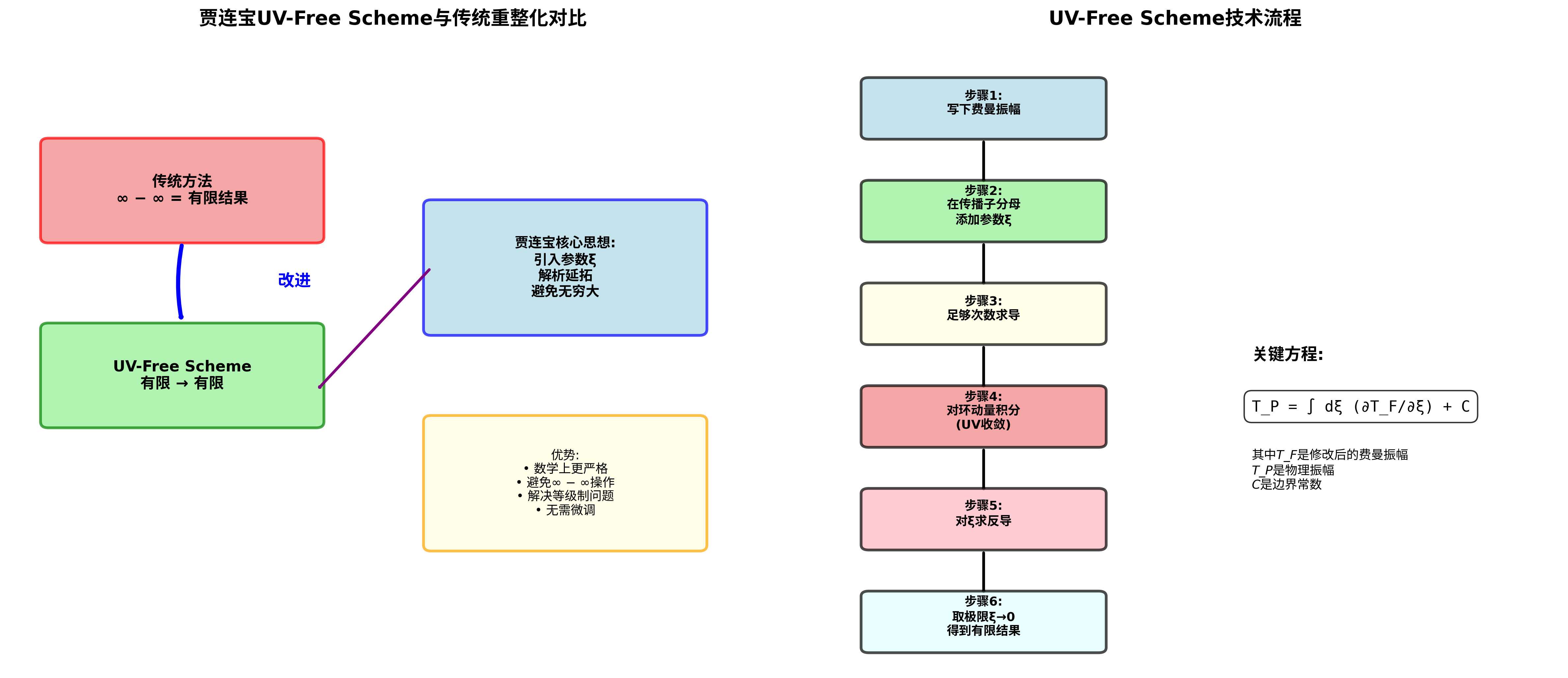
贾连宝UV-Free Scheme可视化
图4：贾连宝UV-Free Scheme与传统重整化方法的对比
"如果相信环的物理贡献是有限的，那么如何找到一种适当的方法来直接获得没有UV发散的物理有限结果？这是一个开放问题。本文探索了一种推导有限环贡献的新方法，无需UV发散。"
—— 贾连宝 (2026)

5.2 技术方法详解

核心方程

贾连宝提出，具有传播子的过渡振幅可以用以下方程描述：

TP = ∫ dξ (∂TF/∂ξ) + C

其中：

  • TP：物理过渡振幅
  • TF：修改后的费曼振幅（在传播子分母中添加参数ξ）
  • ξ：引入的参数，最终取极限ξ → 0
  • C：边界常数，由重整化条件确定

计算步骤

  1. 写下费曼振幅：使用费曼规则写出过渡振幅
  2. 添加参数ξ：在传播子分母中添加参数ξ
  3. 求导：对参数ξ求足够次数的导数
  4. 积分：对环动量积分（此时积分是UV收敛的）
  5. 反导：对ξ求反导
  6. 取极限：取ξ → 0的极限，得到有限结果

5.3 解决等级制问题：Higgs质量的预言

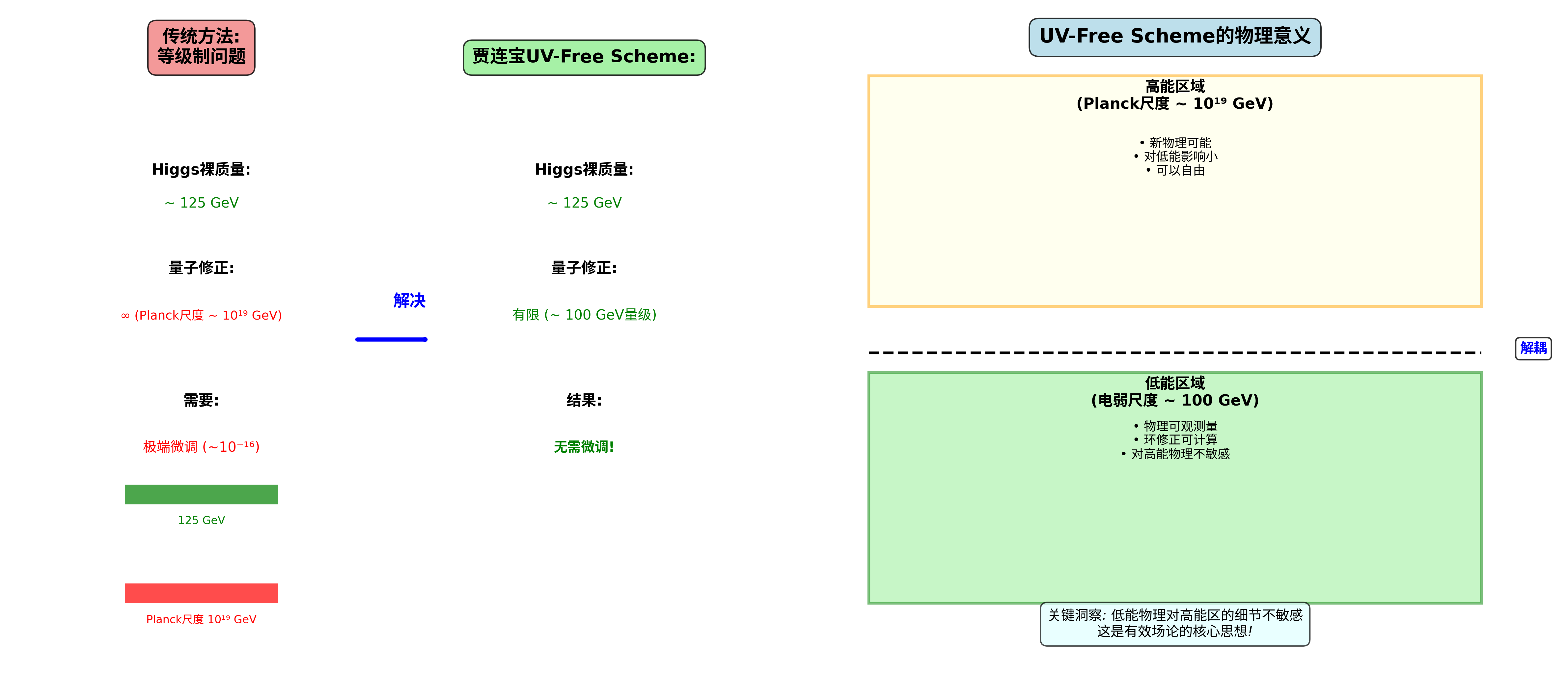
等级制问题解决方案
图5：贾连宝方法如何解决Higgs质量的等级制问题

Higgs质量的等级制问题

问题描述：在标准模型中，Higgs玻色子的质量约为125 GeV。然而，根据传统量子场论，Higgs质量应该接收来自高能尺度（如Planck尺度 ~10¹⁹ GeV）的量子修正，这些修正应该是巨大的，导致Higgs质量需要极端的微调（约10⁻¹⁶精度）才能保持在观测值附近。

贾连宝的解决方案：在UV-Free Scheme中，环修正对Higgs质量的贡献不是非常大，而是有限的，并且与电弱尺度相当。因此，125 GeV的Higgs质量可以在标准模型内自然获得，无需引入新的物理机制或极端的微调。

10⁻¹⁶
传统方法需要的微调精度
无需微调
UV-Free Scheme的结果
125 GeV
预测的Higgs质量

5.4 应用实例与验证

两粒子散射的单圈修正

在φ⁴理论中，两粒子散射的单圈振幅在传统方法中是对数发散的。使用UV-Free Scheme：

  • 在传播子分母中添加参数ξ
  • 对ξ求导后，环动量积分变为UV收敛
  • 积分后求反导
  • 取ξ → 0极限，得到有限结果

最终结果与维数正规化加重整化的结果相同，但计算过程中没有出现UV发散，也不需要∞−∞的操作。

轴矢流的守恒破缺

轴矢流jμ5在质量less费米子情况下不守恒：

∂μjμ5 = (e²/16π²)εμνρσFμνFρσ

使用UV-Free Scheme计算轴矢流→两个光子的跃迁，得到与Adler-Bell-Jackiw异常方程一致的结果，但计算过程更加清晰，没有无穷大的困扰。

QED中的电子自能修正

在量子电动力学中，电子自能修正在传统方法中是对数发散的。使用UV-Free Scheme：

  • 修改光子传播子，添加参数ξ
  • 计算修改后的自能积分
  • 对ξ求反导
  • 应用壳上重整化条件

得到与实验吻合的有限结果，无需通过维数正规化。

5.5 物理意义与哲学

"在UV-Free Scheme中，低能过程中的环修正是局域的，对来自非常高能尺度（如Planck尺度）的环动量贡献不敏感，UV区域可能存在的新物理是自由的。"
—— 贾连宝

深刻的物理洞察

贾连宝的工作揭示了量子场论的一个重要特性：局域性。低能物理过程主要由低能自由度决定，高能自由度的具体细节对低能物理影响有限。这与有效场论的观点一致，但UV-Free Scheme提供了一个更直接、更数学化的实现方式。

自下向上的物理图像：与传统重整化的自上向下图像不同（从包含无穷大的裸参数出发，通过减除得到物理结果），UV-Free Scheme采用自下向上的图像：从局域的、有限的物理量出发，构建完整的理论。

5.6 研究背景与学术影响

作者背景

  • 贾连宝，西南科技大学数学与物理学院
  • 南开大学物理学院
  • 重庆大学物理系，重庆强耦合物理重点实验室
  • 通讯邮箱：jialb@mail.nankai.edu.cn

论文信息

  • 期刊：Communications in Theoretical Physics
  • 卷期：78 (2026) 015201
  • DOI：https://doi.org/10.1088/1572-9494/adf49d
  • 接收日期：2024年9月10日
  • 发表日期：2025年9月9日

重要声明

贾连宝的UV-Free Scheme代表了对量子场论中无穷大问题的全新思考方式。虽然该方法在数学上的严格性还需要进一步验证，但它为解决长期困扰物理学家的基本问题提供了新的可能性，值得深入研究和探索。

VI. 其他新重整化方案研究进展

6.1 有限重整化方案

"费曼在1960年代就提出了有限重整化的可能性。最近的研究表明，使用新的数学技术，可以实现不引入无穷大的重整化程序。"
—— 相关研究文献

6.2 数学新方法

Hopf
代数方法
BPHZ
改进方案
EG
因果方法

近期重要进展

  • 因果时空方法：Epstein-Glaser方法的发展，基于因果性避免发散
  • Hopf代数方法：Connes和Kreimer发展的代数结构，为重整化提供数学基础
  • 维数正规化替代方案：避免解析延拓到非物理维度的新方法
  • 光锥量子化：在光锥坐标系中量子化，简化重整化程序
  • 非对易几何：使用非对易几何框架处理量子场论

6.3 实验检验与验证

新重整化方案的成功不仅在于数学上的优雅，更在于能否做出与实验吻合的预测。目前的挑战包括：

  • 计算高阶修正并与实验比较
  • 处理非微扰效应
  • 扩展到标准模型的其他部分
  • 与量子引力理论的协调

VII. 哲学与方法论反思

6.1 数学与物理的关系

量子场论中无穷大的问题触及了物理学中的一个基本问题：数学与物理现实的关系是什么？

"在物理学中，我们使用数学作为工具来描述自然。但是当数学给出无穷大时，我们应该责怪数学还是责怪物理理论？"
—— 物理学哲学讨论

6.2 科学理论的评判标准

预测
准确性
数学
优雅性
概念
清晰度

关于科学理论的评价标准

量子场论的例子引发了关于科学理论评价的深层问题：

  • 经验成功 vs 数学严格性：一个理论可以在经验上非常成功，但数学上存在问题
  • 实用主义 vs 严格性：费曼的实用主义方法与狄拉克的严格性要求之间的张力
  • 历史发展：科学理论往往先以不完美的形式出现，然后逐渐完善
  • 有效性的范围：所有理论都有其适用范围，超出这个范围可能需要新的理论

6.3 未来展望

未解决的问题

  • 量子引力：如何在量子引力理论中处理类似的发散问题
  • 弦理论：弦理论中的重整化与点粒子理论的差异
  • 非微扰效应：许多物理现象需要非微扰方法，这超出了传统重整化的范围
  • 统一理论：在统一所有基本相互作用的理论中，无穷大问题的处理

VIII. 结论与建议

7.1 主要发现总结

必要
重整化的必要性
尽管存在数学和哲学上的质疑，重整化是处理量子场论中无穷大的必要技术，并且取得了惊人的成功。
历史
历史发展的必然性
从早期的困惑到现代的理解，重整化理论的发展反映了科学理论逐渐成熟的历史过程。
深化
现代理解的深化
有效场论和重整化群理论为理解无穷大提供了更深刻的视角，将重整化从"技术"提升为"原理"。

7.2 未来研究方向

数学
严格化
新方案
探索
实验
检验

7.3 对物理学教育的启示

教育建议

  • 历史教学：教授物理时应该包括历史背景，让学生理解理论发展的过程
  • 批判性思维：鼓励学生像狄拉克和费曼一样质疑现有理论，而不仅仅是接受
  • 理论与实践：平衡数学严格性和物理直觉，理解两者的互补关系
  • 开放问题：向学生展示科学中的未解决问题，激发他们的研究兴趣

下载资源

获取本报告的完整资料，包括详细的数学推导和历史文献

下载大纲 (Markdown) 下载时间线图表 下载概念图

参考文献